Morris遍历作用
Morris遍历是用于节省二叉树遍历的时候的空间的
如果是常规的二叉树遍历,不管是递归还是迭代实现的,空间复杂度都是O(M),M是树的高度,因为每一个节点都会回到它三次,遍历的先后序的不同就是在这三次中的哪一次访问这个结点
//第一次
process(node.left)
//第二次
process(node.right)
//第三次
因此需要有一个栈存储当前节点,当回到当前节点时则从栈中弹出
栈中会压入多少个节点,由树高决定
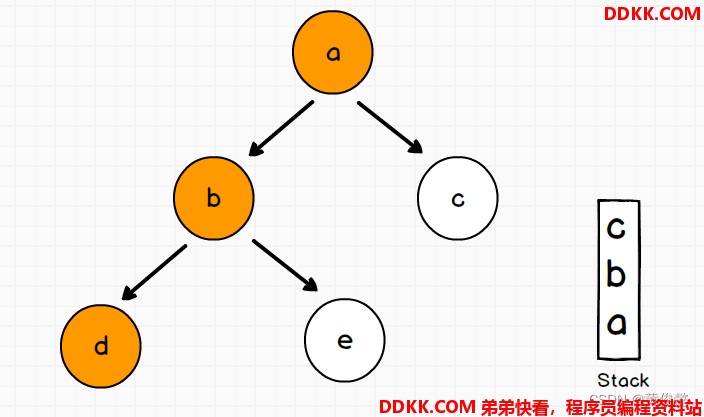
而Morris遍历就是对二叉树遍历的空间复杂的优化
Morris遍历的细节
Morris遍历是利用树中节点的空闲右指针
假设来到当前节点cur,开始时cur来到头节点位置
1)如果cur没有左孩子,cur向右移动(cur = cur.right)
2)如果cur有左孩子,找到左子树上最右的节点mostRight
a.如果mostRight的右指针指向空,让其指向cur,然后cur向左移动(cur = cur.left)
b.如果mostRight的右指针指向cur,让其指向null,然后cur向右移动(cur = cur.right)
3)cur为空是遍历停止
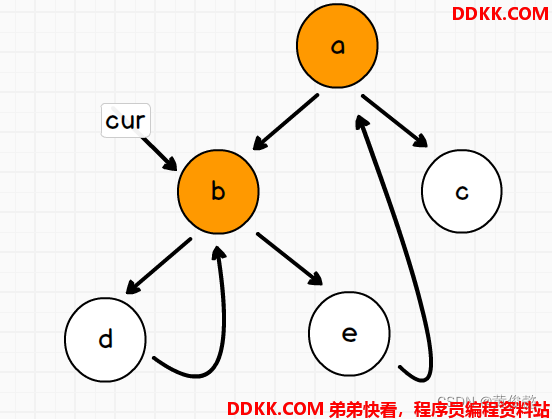
其实就是用当前节点的左子树的最右节点的右指针状态,标记是第几次来到当前节点
如果当前节点的左子树的最右节点的右指针为null,表示第一次来到当前节点
如果当前节点的左子树的最右节点的右指针指向当前节点,表示之前已经来过一次,现在是第二次来到当前节点
Morris遍历代码实现
/**
* Morris序列
* @param head
*/
public static void process(Node head) {
if (head == null) return;
Node cur = head; // cur指针,一开始在头节点
Node mostRight = null; // 左子树的最右节点
while (cur != null) {
mostRight = cur.left; // 左树
if (mostRight != null) {
// 左树不为空
// 一直往右
while (mostRight.right != null && mostRight.right != cur) mostRight = mostRight.right;
// 左子树的最右节点的右指针为空,第一次来
if (mostRight.right == null) {
// 指向当前节点,然后cur往左移
mostRight.right = cur;
cur = cur.left;
continue;
} else {
// 左子树的最右节点的右指针不为空,第二次来,置空mosrtRight的right指针
mostRight.right = null;
}
}
// cur指针往右
cur = cur.right;
}
}
Morris先序遍历
/**
* Morris先序遍历
* @param head
*/
public static void processPre(Node head) {
if (head == null) return;
Node cur = head;
Node mostRight = null;
while (cur != null) {
mostRight = cur.left;
if (mostRight != null) {
while (mostRight.right != null && mostRight.right != cur) mostRight = mostRight.right;
if (mostRight.right == null) {
mostRight.right = cur;
// 有左树的节点,第一次来到的时候就打印
System.out.println(cur.value);
cur = cur.left;
continue;
} else {
mostRight.right = null;
}
} else {
// 没有左树的节点,直接打印
System.out.println(cur.value);
}
cur = cur.right;
}
}
Morris中序遍历
/**
* Morris中序遍历
* @param head
*/
public static void processIn(Node head) {
if (head == null) return;
Node cur = head;
Node mostRight = null;
while (cur != null) {
mostRight = cur.left;
if (mostRight != null) {
while (mostRight.right != null && mostRight.right != cur) mostRight = mostRight.right;
if (mostRight.right == null) {
mostRight.right = cur;
cur = cur.left;
continue;
} else {
mostRight.right = null;
}
}
// 不管是否有左树,都会来到这里,有左树的第二次会来到这里
System.out.println(cur.value);
cur = cur.right;
}
}
Morris后序遍历
/**
* Morris后续遍历
* @param head
*/
public static void processPost(Node head) {
if (head == null) return;
Node cur = head;
Node mostRight = null;
while (cur != null) {
mostRight = cur.left;
if (mostRight != null) {
while (mostRight.right != null && mostRight.right != cur) mostRight = mostRight.right;
if (mostRight.right == null) {
mostRight.right = cur;
cur = cur.left;
continue;
} else {
mostRight.right = null;
//每次第二次返回当该节点时,打印它的左树的右边界,以逆序的方式
printEdge(cur.left);
}
}
cur = cur.right;
}
//最后逆序打印整棵树的右边界
printEdge(head);
}
// 逆序打印树的右边界
private static void printEdge(Node head) {
// 树的右边界,链表反转
Node tail = reverse(head);
Node cur = tail;
// 遍历链表打印
while (cur != null) {
System.out.println(cur.value);
cur = cur.right;
}
// 把链表返回回去
reverse(tail);
}
// 反转树的右边界链表
private static Node reverse(Node head) {
Node pre = null;
Node cur = head;
Node right = null;
while (cur != null) {
right = cur.right;
cur.right = pre;
pre = cur;
cur = right;
}
return pre;
}
Morris遍历判断一颗树是否是搜索二叉树
/**
* Morris遍历判断一颗树是否是搜索二叉树
* Created by huangjunyi on 2022/9/10.
*/
public class Morris02 {
private static class Node {
Node left;
Node right;
int value;
}
public static boolean isBST(Node head) {
if (head == null) return true;
Node cur = head;
Node mostRight = null;
//拿一个变量preValue记录前一个遍历到的结点的值
Integer preValue = null;
while (cur != null) {
mostRight = cur.left;
if (mostRight != null) {
while (mostRight.right != null && mostRight.right != cur) mostRight = mostRight.right;
if (mostRight.right == null) {
mostRight.right = cur;
cur = cur.left;
continue;
} else {
mostRight.right = null;
}
}
// 以Morris中序遍历的顺序,判果前一个节点的值是否比当前节点大,是则返回false,代表不是BST
// 这里是不在乎树的指针被改乱掉的,所有直接返回false,否则就不能直接返回false,要遍历完再返回
if (preValue != null && cur.value <= preValue) return false;
preValue = cur.value;
cur = cur.right;
}
return true;
}
}
Morris遍历求一棵树离头节点最近的叶节点的高度
/**
* Morris遍历求一棵树离头节点最近的叶节点的高度
* Created by huangjunyi on 2022/9/10.
*/
public class Morris03 {
private static class Node {
Node left;
Node right;
int value;
}
public static int getMinHigh(Node head) {
if (head == null) return 0;
Node cur = head;
Node mostRight = null;
int minHigh = Integer.MAX_VALUE;
int leftRightBoardsize = -1;
int curLevel = 0; // 当前节点层数
while (cur != null) {
mostRight = cur.left;
leftRightBoardsize = 1;
if (mostRight != null) {
//当前节点有左树
while (mostRight.right != null && mostRight.right != cur) {
// 寻找当前节点的左树的最右节点的同时记录左树右边界的节点数
mostRight = mostRight.right;
leftRightBoardsize++;
}
if (mostRight.right == null) {
// 进入这里,表示第一次来到当前节点
// 把左树最右节点的右指针修改为指向当前节点,cur指针往左节点移动
mostRight.right = cur;
curLevel++;
cur = cur.left;
continue;
} else {
// 进入这里,表示第二次来到当前节点
// 看看当前节点的左子树的最右节点的左节点是否为空,为空代表它是叶子节点
// 发现左树最右节点是子节点,清算一下,更新minHigh
if (mostRight.left == null) {
minHigh = Math.min(minHigh, curLevel);
}
// curLevel当前是左树最右节点的高度,减去leftRightBoardsize左树右边界节点数,得出当前节点高度
curLevel -= leftRightBoardsize;
// 恢复当前节点的左子树的最右节点的右指针
mostRight.right = null;
}
} else {
//当前节点没有左树,单纯层数++
curLevel++;
}
cur = cur.right;
}
return minHigh;
}
}
什么时候用Morris遍历
笔试的时候不要用,用最普通最好实现的递归就OK
面试的时候可以使用Morris遍历,进行优化
如果严格需要左右子树的答案,才能整合出当前节点的答案,那么只能用递归,不能用Morris遍历
如果不是严格依赖左右子树的答案的,可以用Morris遍历进行优化