有序表
存储key-value键值对
根据key进行排序,保证加入的元素在表中有序排列
二叉搜索数
二叉搜索树的特点
最简单的有序表
树状
每个节点的key都大于它的左子树的key
每个节点的key都大于它的右字树的key
二叉搜索树节点的删除
如果是叶子节点,直接删除。
如果只有一个孩子,有左无右、有右无左,那么让它的孩子替代它。
如果两个孩子都有。找到右树上的最左节点,让这个节点去替代删除的节点,但是注意这个最左节点有可能有右节点,要先把这个右节点挂到它的父节点下。
二叉搜索树的瓶颈
二叉搜索树的瓶颈来自于它的树高
而树高又受添加元素的顺序影响
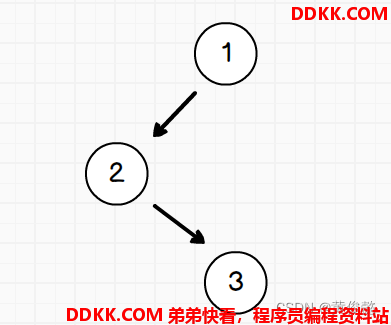
如果添加的顺序是1、2、3、4、5…
那么就会退化回链表
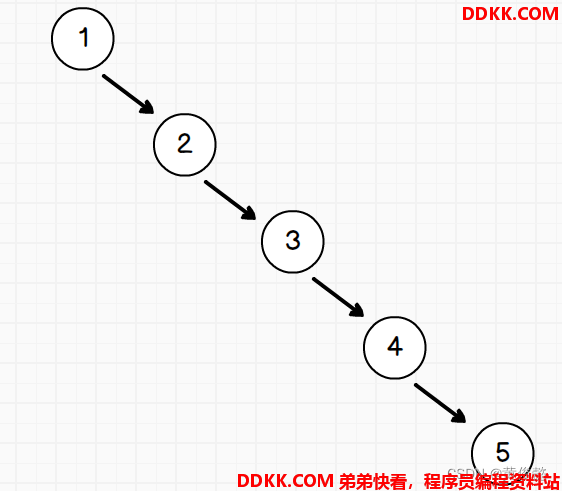
解决办法iu是通过左旋,右旋,使得树保证相对的平衡性
左旋、右旋
左旋还是右旋,看当前头节点往哪边倒下去
当前头节点往左边倒下去的,就是左旋
当前头节点往右边倒下去的,就是右旋
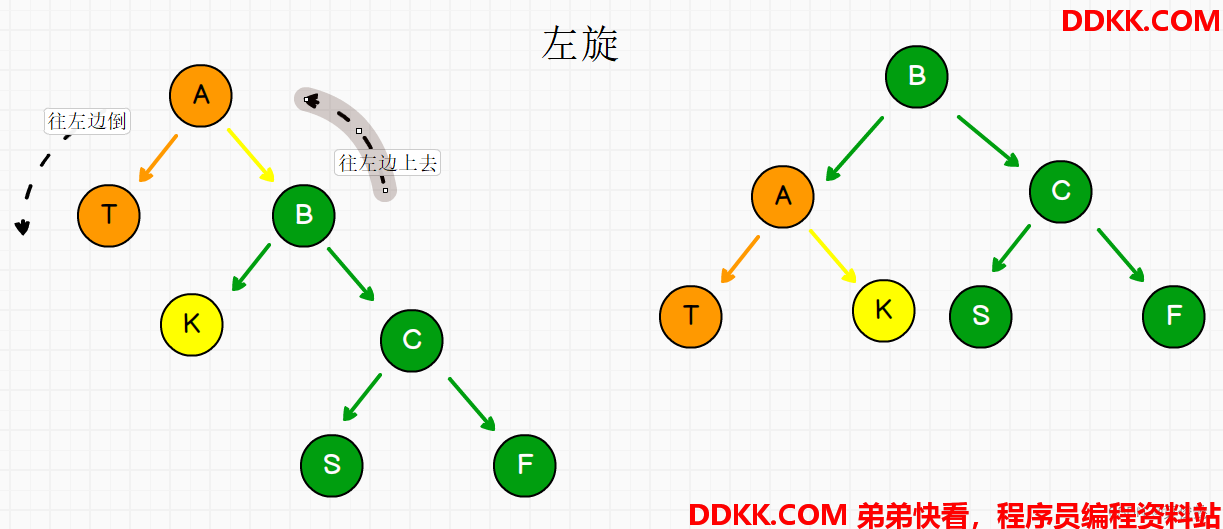
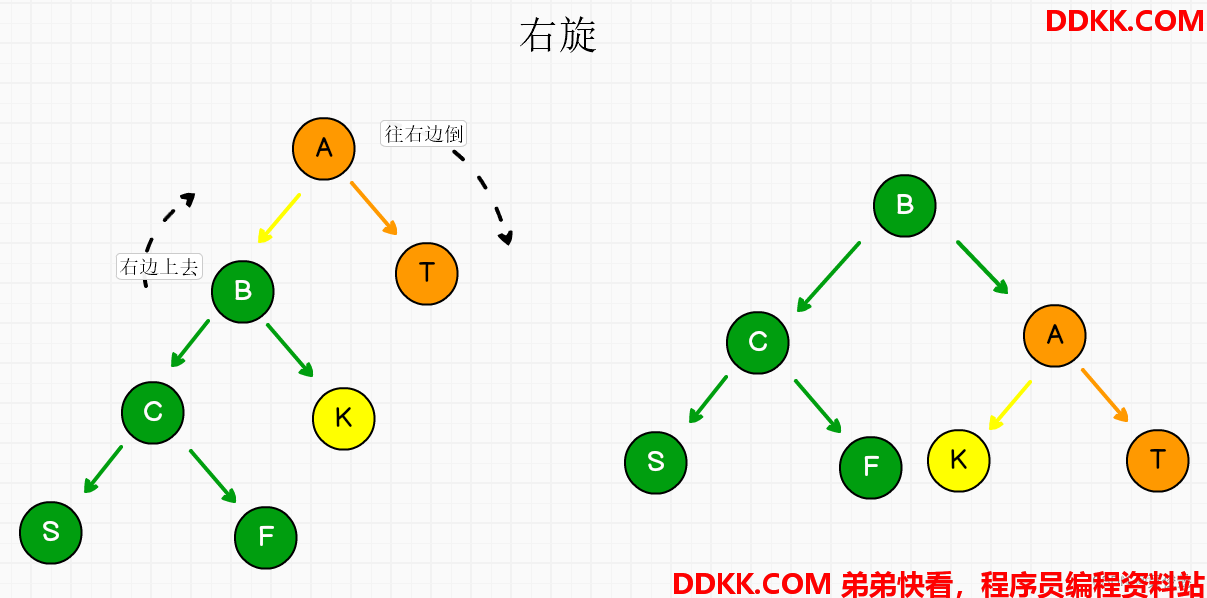
旋转之后,不会破坏搜索二叉树左小右大的性质。
不同的平衡二叉树,AVL数,SB数,红黑树,底层使其变平衡的最基本的操作都是左旋和右旋。
AVL数,SB数,红黑树…,相同点是时间复杂度都是O(logN),不同点在于平衡策略不一样。
AVL树
AVL树的特点
非常严苛的平衡二叉树。
相当于搜索二叉树上打了保证平衡性的补丁。
左树和右树的高度差不超过1。
平衡性被破坏的情况
4种情况:LL型,LR型,RR型,RL型
LL型是指左树高度比右树高度高1以上,而左树上左树的高度比右树的高度高1
RR型是指右树高度比左树高度高1以上,而右树上右树的高度比左树的高度高1
LR型是指左树高度比右树高度高1以上,但是左树上右树的高度比左树的高度高1
RL型是指右树高度比左树高度高1以上,但是右树上左树的高度比右树的高度高1
当左树的高度比右树的高度高1以上,如果左树的左右子树高度相等,视为LL型
当右树的高度比左树的高度高1以上,如果右树的左右子树高度相等,视为RR型
LL型
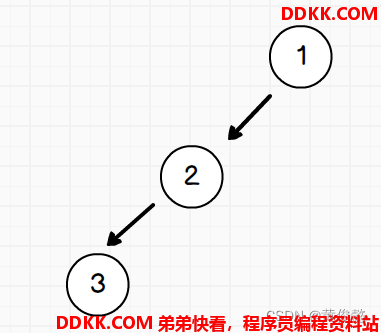
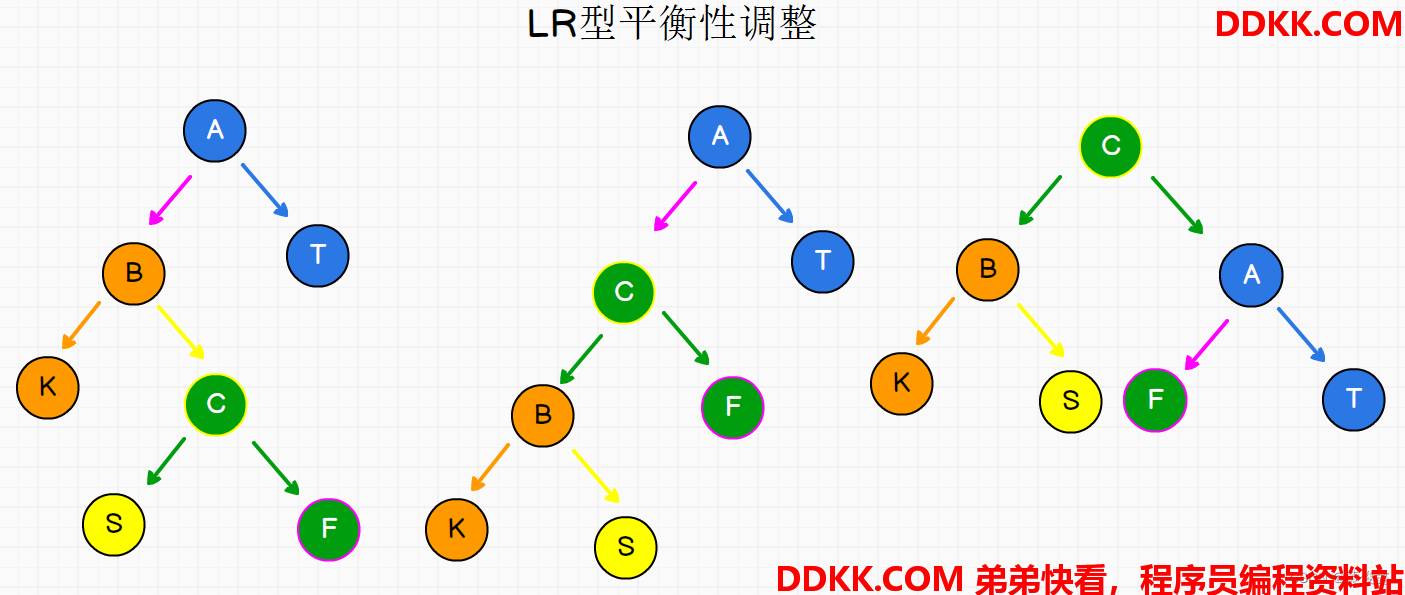
LR型
RR型和RL型依次类推。
LL型平衡性调整:做一次右旋
RR型平衡性调整:做一次左旋
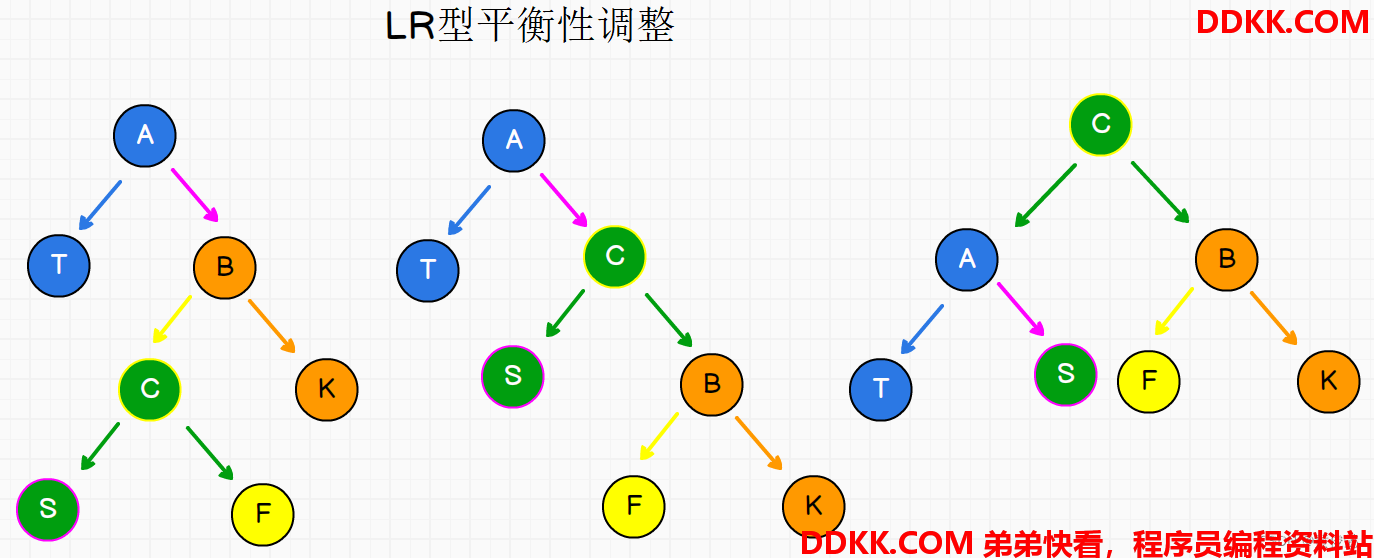
LR型平衡性调整:先左旋,再右旋,让孙子节点上去
RL型平衡性调整:先右旋,在左旋,让孙子节点上去
调整本身是O(1)的时间复杂度。
AVL树平衡性调整策略
添加节点:
当某个节点加入到AVL树中时,加入节点后,往上经过的每一个节点(包括加入节点本身),检查每个节点是否出现破坏平衡性的情况(LL、LR、RL、RR)。
删除节点:
叶子节点,直接删除后,被删除节点原先的位置往上经过的每一个节点都检查一遍。
有左无右,有右无左,拿它的孩子节点替代它,从它的孩子来到的地方开始查起。
有左有右,拿后继节点替代它,后继节点原先的位置往上都要查。
代码实现
/**
* 完全平衡二叉树
* Created by huangjunyi on 2022/9/16.
*/
public class AVLTree<K extends Comparable<K>, V> {
public static class AVLTreeNode<K extends Comparable<K>, V> {
private K key; // key
private V value; // value
private AVLTreeNode left; // 左孩子
private AVLTreeNode right; // 右孩子
private int high; // 树高度
}
// 头节点
private AVLTreeNode<K, V> root;
/**
* 添加节点
* @param key
* @param value
*/
public void add(K key, V value) {
if (key == null) return;
// add方法带返回值,因为有可能换头部,换了要接住新头
this.root = add(this.root, key, value);
}
/**
* 添加节点
* @param cur
* @param key
* @param value
* @return
*/
private AVLTreeNode<K, V> add(AVLTreeNode<K, V> cur, K key, V value) {
if (cur == null) {
// 当前节点null,建出新节点返回
AVLTreeNode<K, V> node = new AVLTreeNode<>();
node.key = key;
node.value = value;
node.high = 1;
return node;
}
if (cur.key.compareTo(key) > 0) {
// 当前节点key大于加入的key,往左树挂,有可能换头,所以cur.left接住
cur.left = add(cur.left, key, value);
} else if (cur.key.compareTo(key) < 0) {
// 当前节点key小于加入的key,往右树挂,有可能换头,所以cur.right接住
cur.right = add(cur.right, key, value);
} else {
// nothing to do
}
// 调整高度
cur.high = Math.max(cur.left != null ? cur.left.high : 0, cur.right != null ? cur.right.high : 0) + 1;
// 检查平衡性,如果平衡性被破坏了,调整
cur = maintain(cur);
return cur;
}
public V get(K key) {
if (key == null) return null;
AVLTreeNode<K, V> node = findLastIndex(key);
if (node != null && node.key.compareTo(key) == 0) return node.value;
return null;
}
private AVLTreeNode<K, V> findLastIndex(K key) {
AVLTreeNode<K, V> pre = root;
AVLTreeNode<K, V> cur = root;
while (cur != null) {
pre = cur;
if (cur.key.compareTo(key) > 0) cur = cur.left;
else if (cur.key.compareTo(key) < 0) cur = cur.right;
else break;
}
return pre;
}
public AVLTreeNode<K, V> findLastNoSmallIndex(K key) {
AVLTreeNode<K, V> pre = null;
AVLTreeNode<K, V> cur = root;
while (cur != null) {
if (cur.key.compareTo(key) == 0) {
pre = cur;
break;
} else if (cur.key.compareTo(key) > 0) {
pre = cur;
cur = cur.left;
} else {
cur = cur.right;
}
}
return pre;
}
public AVLTreeNode<K, V> findLastNoBigIndex(K key) {
AVLTreeNode<K, V> pre = null;
AVLTreeNode<K, V> cur = root;
while (cur != null) {
if (cur.key.compareTo(key) == 0) {
pre = cur;
break;
} else if (cur.key.compareTo(key) > 0) {
cur = cur.left;
} else {
pre = cur;
cur = cur.right;
}
}
return pre;
}
public void put(K key, V value) {
if (key == null) return;
AVLTreeNode<K, V> node = findLastIndex(key);
if (node != null && node.key.compareTo(key) == 0) node.value = value;
else add(key, value);
}
public void remove(K key) {
if (key == null) return;
this.root = delete(this.root, key);
}
/**
* 删除节点
* @param cur
* @param key
* @return
*/
private AVLTreeNode<K, V> delete(AVLTreeNode<K, V> cur, K key) {
// 没有命中,返回null,不删
if (cur == null) return null;
if (cur.key.compareTo(key) > 0) {
// 当前节点key比要删的key大,走左边
cur.left = delete(cur.left, key);
} else if (cur.key.compareTo(key) < 0) {
// 当前节点key比要删的key小,走右边
cur.right = delete(cur.right, key);
} else {
// 命中了,要删这个节点
if (cur.left == null && cur.right == null) {
// 无左无右,直接删除
cur = null;
} else if (cur.left != null && cur.right == null) {
// 有左无右,左孩子接替
cur = cur.left;
} else if (cur.left == null && cur.right != null) {
// 无左有右,右孩子接替
cur = cur.right;
} else {
// 有左有右,后继节点接替
// 寻找后继节点,右树上的最左节点
AVLTreeNode<K, V> successor = cur.right;
while (successor.left != null) successor = successor.left;
// 现在找到了后继节点,先在右树上,把后继节点删除
cur.right = delete(cur.right, successor.key);
// 后继节点接住删除节点的左右孩子
successor.left = cur.left;
successor.right = cur.right;
// 后继节点接替当前节点
cur = successor;
}
}
// 高度调整
cur.high = Math.max(cur.left != null ? cur.left.high : 0, cur.right != null ? cur.right.high : 0) + 1;
// 平衡性检查
return maintain(cur);
}
public boolean containsKey(K key) {
if (key == null) return false;
AVLTreeNode<K, V> node = findLastIndex(key);
if (node != null && node.key.compareTo(key) == 0) return true;
return false;
}
private AVLTreeNode<K, V> maintain(AVLTreeNode<K, V> cur) {
if (cur == null) return null;
int leftHigh = cur.left != null ? cur.left.high : 0;
int rightHith = cur.right != null ? cur.right.high: 0;
if (Math.abs(leftHigh - rightHith) > 0) {
// 左右树高差大于1?
if (leftHigh > rightHith) {
// 左树高?
int leftleftHigh = cur.left.left != null ? cur.left.left.high : 0;
int leftRightHigh = cur.left.right != null ? cur.left.right.high : 0;
if (leftleftHigh >= leftRightHigh) {
// LL型
cur = rightRotate(cur); // 一次右旋即可
} else {
// LR型
cur.left = leftRotate(cur.left); // 先左旋
cur = rightRotate(cur); // 再右旋
}
} else {
// 右树高?
int rightRightHigh = cur.right.right != null ? cur.right.right.high : 0;
int rightLeftHigh = cur.right.left != null ? cur.right.left.high : 0;
if (rightRightHigh >= rightLeftHigh) {
// RR型
cur = leftRotate(cur); // 一次左旋即可
} else {
// RL型
cur.right = rightRotate(cur.right); // 先右旋
cur = leftRotate(cur); // 再左旋
}
}
}
return cur;
}
/**
* 左旋
*/
private AVLTreeNode leftRotate(AVLTreeNode<K, V> cur) {
AVLTreeNode<K, V> curRight = cur.right;
cur.right = curRight.left;
curRight.left = cur;
cur.high = Math.max(cur.left != null ? cur.left.high : 0, cur.right != null ? cur.right.high : 0) + 1;
curRight.high = Math.max(curRight.left != null ? curRight.left.high : 0, curRight.right != null ? curRight.right.high : 0) + 1;
return curRight;
}
/**
* 右旋
*/
private AVLTreeNode<K, V> rightRotate(AVLTreeNode<K, V> cur) {
AVLTreeNode<K, V> curLeft = cur.left; // curLeft 左孩子
cur.left = curLeft.right; // 左指针,指向左孩子的右
curLeft.right = cur; // 左孩子的右,指向自己
// 自己调整高度
cur.high = Math.max(cur.left != null ? cur.left.high : 0, cur.right != null ? cur.right.high : 0) + 1;
// 原孩子调整高度
curLeft.high = Math.max(curLeft.left != null ? curLeft.left.high : 0, curLeft.right != null ? curLeft.right.high : 0) + 1;
// 返回新头部
return curLeft;
}
}
有序表和AVL树的关系
有序表是接口,AVL树是实现。
SizeBalanceTree
SB树特点
继承自搜索二叉树
任何叔叔节点为头的子树的节点个数不小于侄子树的节点个数
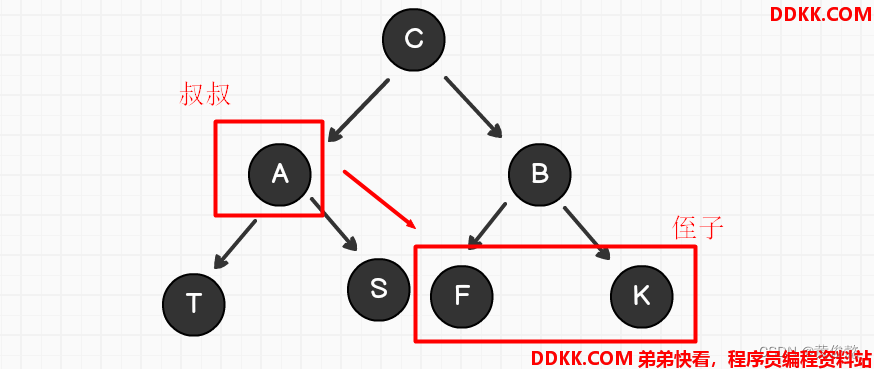
也有四种破环平衡性的情况
删除节点时不需要做平衡性检查和调整,只在增加节点时做平衡性检查和调整。
平衡性被破坏的情况
LL型
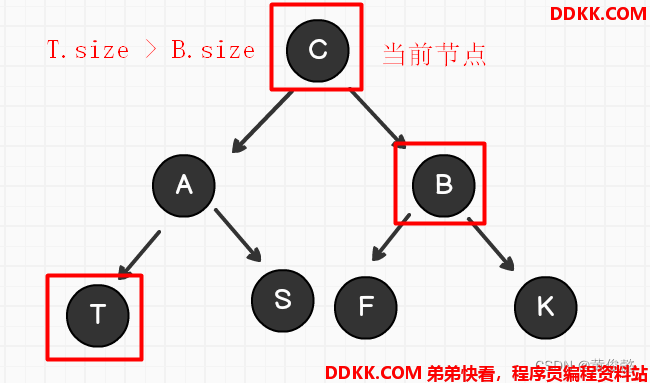
LR型
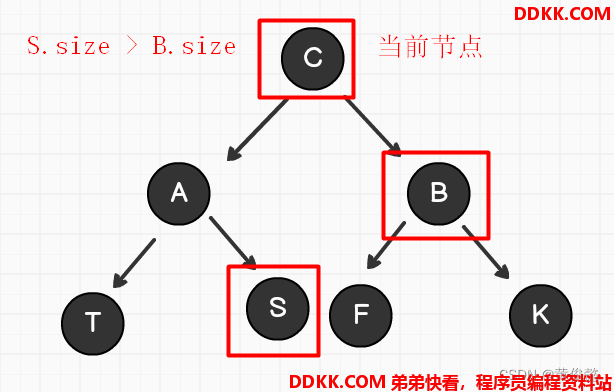
RL型
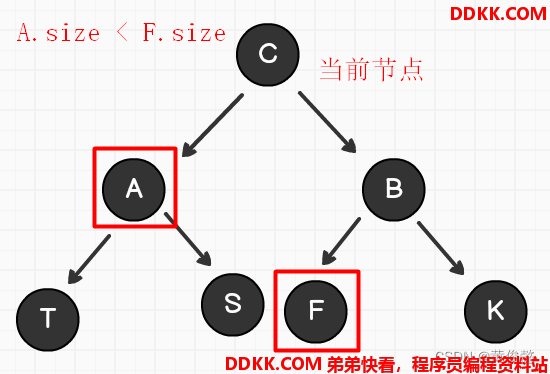
RR型
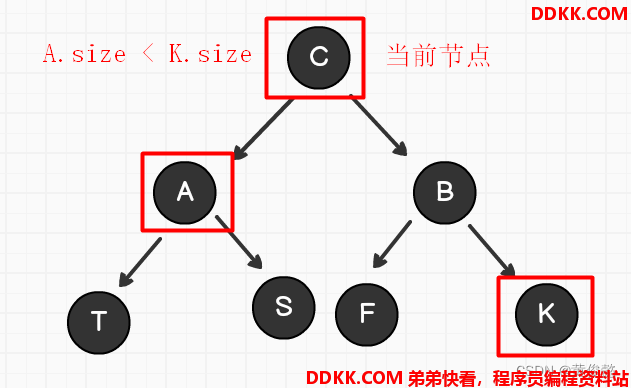
平衡性检查和调整
平衡性检查和AVL树一样,也是沿途往上都要检查。
平衡性被破坏的四种情况,调整动作和AVL树也一样(LL一次右旋,LR先左旋再右旋,…)。
区别就是调整完后,哪些节点的子节点换了,要递归调用换了子节点的节点的平衡性调整。
而且删除节点时不需要做平衡性检查和调整,只在增加节点时做平衡性检查和调整。
代码实现
/**
* SB树
* Created by huangjunyi on 2022/9/17.
*/
public class SizeBalancedTree<K extends Comparable<K>, V> {
public static class SizeBalancedTreeNode<K extends Comparable<K>, V> {
private K key; // key
private V value; // value
private SizeBalancedTreeNode<K, V> left; // 左孩子
private SizeBalancedTreeNode<K, V> right; // 右孩子
private int size; // 树节点个数
public SizeBalancedTreeNode(K key, V value, int size) {
this.key = key;
this.value = value;
this.size = size;
}
}
private SizeBalancedTreeNode<K, V> root; // 树根节点
public void put(K key, V value) {
if (key == null) return;
SizeBalancedTreeNode<K, V> node = findLastIndex(key);
if (node != null && node.key.compareTo(key) == 0) node.value = value;
else this.root = add(this.root, key, value);
}
private SizeBalancedTreeNode<K, V> add(SizeBalancedTreeNode<K, V> cur, K key, V value) {
if (cur == null) {
return new SizeBalancedTreeNode<>(key, value, 1);
}
if (key.compareTo(cur.key) < 0) {
cur.left = add(cur.left, key, value);
} else {
cur.right = add(cur.right, key, value);
}
// 加完节点,沿途的节点size都++
cur.size++;
// 沿途都做平衡性检查
return maintain(cur);
}
public void remove(K key) {
if (key == null) return;
this.root = delete(this.root, key);
}
private SizeBalancedTreeNode<K, V> delete(SizeBalancedTreeNode<K, V> cur, K key) {
if (cur == null) return null;
// 删的时候,沿途size都--
cur.size--;
if (key.compareTo(cur.key) < 0) {
cur.left = delete(cur.left, key);
} else if (key.compareTo(cur.key) > 0) {
cur.right = delete(cur.right, key);
} else {
if (cur.left == null && cur.right == null) {
cur = null;
} else if (cur.left != null && cur.right == null) {
cur = cur.left;
} else if (cur.left == null && cur.right != null) {
cur = cur.right;
} else {
SizeBalancedTreeNode<K, V> successor = cur.right;
while (successor.left != null) successor = successor.left;
cur.right = delete(cur.right, successor.key);
successor.left = cur.left;
successor.right = cur.right;
successor.size = cur.size;
cur = successor;
}
}
// 删除不做平衡性检查和调整
return cur;
}
public V get(K key) {
if (key == null) return null;
SizeBalancedTreeNode<K, V> node = findLastIndex(key);
if (node != null && node.key.compareTo(key) == 0) return node.value;
return null;
}
/**
* 平衡性检查和调整
* @param cur
* @return
*/
private SizeBalancedTreeNode<K, V> maintain(SizeBalancedTreeNode<K, V> cur) {
if (cur == null) return null;
int curLeftSize = cur.left != null ? cur.left.size : 0; // 左孩子size
int curLeftLeftSize = cur.left != null && cur.left.left != null ? cur.left.left.size : 0; // 左左孩子大小
int curLeftRightSize = cur.left != null && cur.left.right != null ? cur.left.right.size : 0; // 左右孩子大小
int curRightSize = cur.right != null ?cur.right.size : 0; // 右孩子大小
int curRightRightSize = cur.right != null && cur.right.right != null ? cur.right.right.size : 0; // 右右孩子大小
int curRightLeftSize = cur.right != null && cur.right.left != null ? cur.right.left.size : 0; // 右左孩子大小
if (curLeftLeftSize > curRightSize) {
// LL型?
cur = rightRotate(cur);
// 换了孩子的节点,递归做平衡性调整
cur.right = maintain(cur.right);
cur = maintain(cur);
} else if (curLeftRightSize > curRightSize) {
// LR型?
cur.left = leftRotate(cur.left);
cur = rightRotate(cur);
// 换了孩子的节点,递归做平衡性调整
cur.left = maintain(cur.left);
cur.right = maintain(cur.right);
cur = maintain(cur);
} else if (curRightRightSize > curLeftSize) {
// RR型?
cur = leftRotate(cur);
// 换了孩子的节点,递归做平衡性调整
cur.left = maintain(cur.left);
cur = maintain(cur);
} else if (curRightLeftSize > curLeftSize) {
// RL型?
cur.right = rightRotate(cur.right);
cur = leftRotate(cur);
// 换了孩子的节点,递归做平衡性调整
cur.left = maintain(cur.left);
cur.right = maintain(cur.right);
cur = maintain(cur);
}
return cur;
}
/**
* 左旋
* @param cur
* @return
*/
private SizeBalancedTreeNode<K, V> leftRotate(SizeBalancedTreeNode<K, V> cur) {
SizeBalancedTreeNode<K, V> right = cur.right;
cur.right = right.left;
right.left = cur;
// size调整
right.size = cur.size;
cur.size = (cur.left != null ? cur.left.size : 0) + (cur.right != null ? cur.right.size : 0) + 1;
return right;
}
/**
* 右旋
* @param cur
* @return
*/
private SizeBalancedTreeNode<K, V> rightRotate(SizeBalancedTreeNode<K, V> cur) {
SizeBalancedTreeNode<K, V> left = cur.left;
cur.left = left.right;
left.right = cur;
// size调整
left.size = cur.size;
cur.size = (cur.left != null ? cur.left.size : 0) + (cur.right != null ? cur.right.size : 0) + 1;
return left;
}
private SizeBalancedTreeNode<K, V> findLastIndex(K key) {
SizeBalancedTreeNode<K, V> pre = this.root;
SizeBalancedTreeNode<K, V> cur = this.root;
while (cur != null) {
pre = cur;
if (key.compareTo(cur.key) < 0) cur = cur.left;
else if (key.compareTo(cur.key) > 0) cur = cur.right;
else break;
}
return pre;
}
private SizeBalancedTreeNode<K, V> findLastNoSmallIndex(K key) {
SizeBalancedTreeNode<K, V> pre = null;
SizeBalancedTreeNode<K, V> cur = this.root;
while (cur != null) {
if (key.compareTo(cur.key) < 0) {
pre = cur;
cur = cur.left;
} else if (key.compareTo(cur.key) > 0) {
cur = cur.right;
} else {
pre = cur;
break;
}
}
return pre;
}
private SizeBalancedTreeNode<K, V> findLastNoBigIndex(K key) {
SizeBalancedTreeNode<K, V> pre = null;
SizeBalancedTreeNode<K, V> cur = this.root;
while (cur != null) {
if (key.compareTo(cur.key) < 0) {
cur = cur.left;
} else if (key.compareTo(cur.key) > 0) {
pre = cur;
cur = cur.right;
} else {
pre = cur;
break;
}
}
return pre;
}
}
跳表
也是有序表,但不是树状,而是链表状的。
每加入一个几点,都随机取一个层数,属于这个节点的层数,层数有多少,节点的后继指针就有多少。
头节点要跟着最高的层数,自己的层数往上涨。
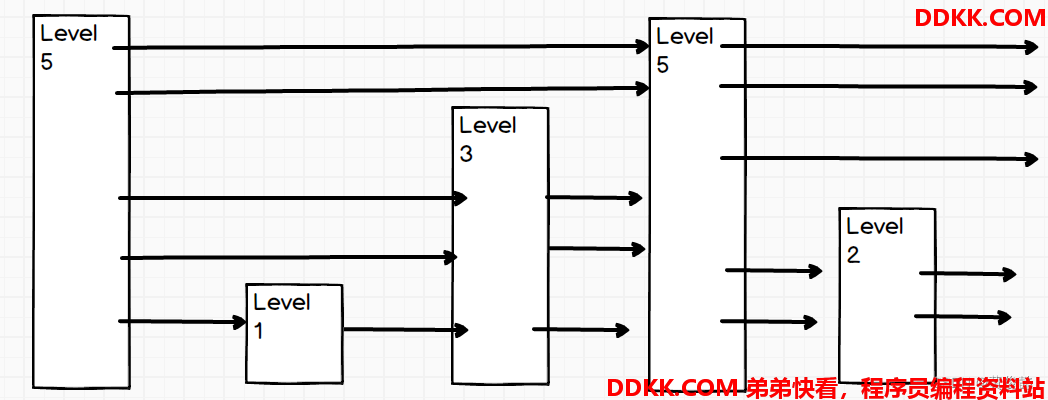
如果要加入一个节点,假设值是77,先随机生成一个层数level,然后从头节点的level层指针开始,沿途寻找每一层比77小又最接近77的,修改后继指针指向新节点。一层挂号切下一层不需要回到开头,直接在当前节点切下一层往下走。
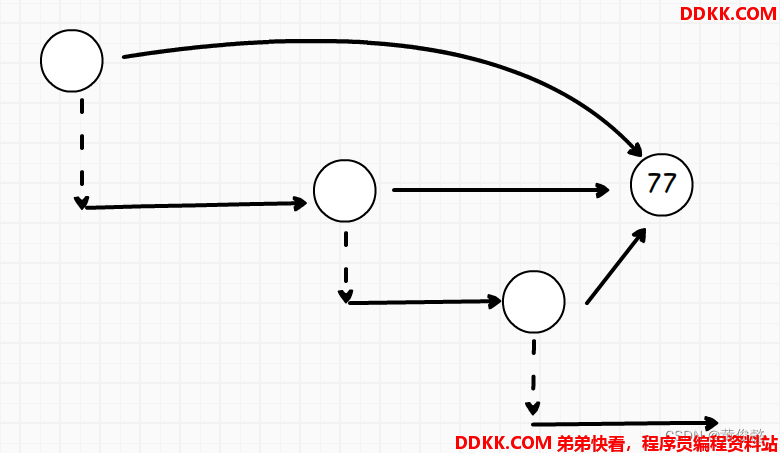
寻找节点时从头节点最顶层level开始沿途寻找,发现下一个节点较大时,也是不需要回到头部,在当前节点切下一层
假如寻找66:
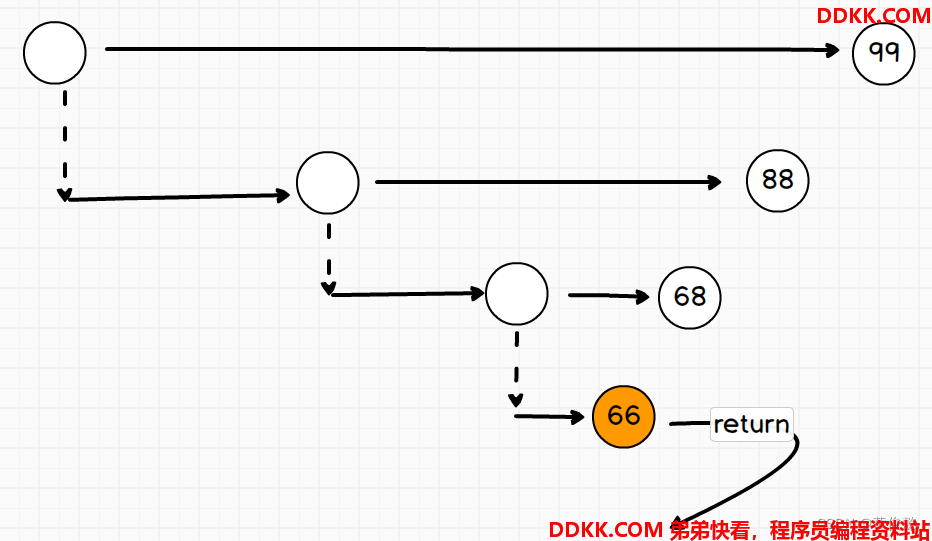
代码实现
/**
* 跳表
* Created by huangjunyi on 2022/9/17.
*/
public class SkipListMap<K extends Comparable<K>, V> {
public static class SkipListNode<K extends Comparable<K>, V> {
private K key; // key 可比较
private V value; // value
private List<SkipListNode> nexts; // 不同层的后继节点们,level数组
public SkipListNode(K key, V value) {
this.key = key;
this.value = value;
nexts = new ArrayList<>();
}
/**
* 比较当前节点key是否小于otherKey
* @param otherKey
* @return
*/
public boolean isKeyLess(K otherKey) {
return otherKey != null && (key == null || key.compareTo(otherKey) < 0);
}
/**
* 比较当前节点key是否与otherKey相等
* @param otherKey
* @return
*/
public boolean isKeyEquals(K otherKey) {
return (key == null && otherKey == null) || (key != null || otherKey != null && key.compareTo(otherKey) == 0);
}
}
private static final double PROBABILITY = 0.5; // 升层概率
private int maxLevel; // 最大层高度
private SkipListNode<K, V> head; // 头节点
public SkipListMap() {
head = new SkipListNode<>(null, null);
head.nexts.add(null);
maxLevel = 0;
}
/**
* 添加 key-value
* @param key
* @param value
*/
public void put(K key, V value) {
if (key == null) return;
// pre 0层上小于key离key最近的最右节点
SkipListNode<K, V> pre = findMostRightLessKeyNode(key);
// pre节点在0层上的下一个节点
SkipListNode<K, V> find = pre.nexts.get(0);
if (find != null && find.isKeyEquals(key)) {
// key是相等的?
find.value = value; // 更新值
} else {
// key是不等的,要挂新节点
SkipListNode<K, V> newNode = new SkipListNode<>(key, value);
// 先随机掷骰子,看能冲到第几层
int newNodeLevel = 0;
while (Math.random() <= PROBABILITY) newNodeLevel++;
// 大于之前所有链表的层数,那么头节点层数要升到一样高
while (maxLevel < newNodeLevel) {
head.nexts.add(null);
maxLevel++;
}
// 初始化新节点的level数组
for (int i = 0; i <= newNodeLevel; i++) {
newNode.nexts.add(null);
}
// 从最左节点开始,从掷骰子的最高层开始,往下一层层挂上新节点
int curLevel = maxLevel;
SkipListNode<K, V> curLevelPre = head;
while (curLevel >= 0) {
// 找到当前层小于key离key最近的最右节点 curLevelPre
curLevelPre = findMostRightLessKeyNodeInCurLevel(curLevelPre, key, curLevel);
// 当前层比掷骰子的层数高,不进去,小于等于才进去挂节点
if (curLevel <= newNodeLevel) {
// 新节点当前层挂curLevelPre在当前层的后继节点
newNode.nexts.set(curLevel, curLevelPre.nexts.get(curLevel));
// curLevelPre在当前层改为挂新节点
curLevelPre.nexts.set(curLevel, newNode);
}
// 切到下一层
curLevel--;
}
}
}
public V get(K key) {
if (key == null) return null;
SkipListNode<K, V> pre = findMostRightLessKeyNode(key);
SkipListNode<K, V> find = pre.nexts.get(0);
if (find != null && find.isKeyEquals(key)) return find.value;
return null;
}
/**
* 是否包含key
* @param key
* @return
*/
public boolean containsKey(K key) {
if (key == null) return false;
// 找到第0层小于key离key最近的最右节点
SkipListNode<K, V> pre = findMostRightLessKeyNode(key);
// 第0层小于key离key最近的最右节点,第0层挂的后继节点find
SkipListNode<K, V> find = pre.nexts.get(0);
// 看find节点key是不是传入的参数key,是的话containsKey返回true
return find != null && find.isKeyEquals(key);
}
public void remove(K key) {
if (containsKey(key)) {
// 包含key?
int curLevel = maxLevel; // 最高层
SkipListNode<K, V> curLevelPre = head; // 最左节点
while (curLevel >= 0) {
// 从最高层到第0层,一层层往下找,然后断连掉
// 找到当前层小于key离key最近的最右节点 curLevelPre
curLevelPre = findMostRightLessKeyNodeInCurLevel(curLevelPre, key, curLevel);
// curLevelPre节点在当前层的后继节点
SkipListNode<K, V> find = curLevelPre.nexts.get(curLevel);
if (find != null && find.isKeyEquals(key)) {
// 是不是要删除的?
curLevelPre.nexts.set(curLevel, find.nexts.get(curLevel)); // 断连,指向下一个
}
// 检查level层是否没节点了,是的话要消掉这一层
if (curLevel != 0 && curLevelPre == head && curLevelPre.nexts.get(curLevel) == null) {
head.nexts.remove(curLevel);
maxLevel--;
}
// 切下一层
curLevel--;
}
}
}
/**
* 从最高层开始找,一直找到第0层小于key离key最近的最右节点
* @param key
* @return
*/
private SkipListNode<K, V> findMostRightLessKeyNode(K key) {
if (key == null) return null;
SkipListNode<K, V> cur = head;
int curLevel = maxLevel;
while (curLevel >= 0) {
cur = findMostRightLessKeyNodeInCurLevel(cur, key, curLevel--);
}
return cur;
}
/**
* 找到当前层小于key离key最近的最右节点
* @param cur
* @param key
* @param curLevel
* @return
*/
private SkipListNode<K, V> findMostRightLessKeyNodeInCurLevel(SkipListNode<K, V> cur, K key, int curLevel) {
SkipListNode<K, V> pre = null;
while (cur != null) {
if (cur.isKeyLess(key)) {
pre = cur;
cur = cur.nexts.get(curLevel);
} else {
break;
}
}
return pre;
}
}
需要改写有序表的题目一
给定一个数组arr,和两个整数a和b(a <= b),
求该数组中有多少个子数组,累加和在[a, b]返回上,
返回达标的子数组数量
/**
* 需要改写有序表的题目一
* 给定一个数组arr,和两个整数a和b(a <= b),
* 求该数组中有多少个子数组,累加和在[a, b]返回上,
* 返回达标的子数组数量
* Created by huangjunyi on 2022/9/17.
*/
public class SortedMap01 {
/**
* SB树实现的Set集合
*/
private static class SizeBalancedTreeSet<E extends Comparable<E>> {
private SizeBalancedTree01<E, Object> map; // SB树实现的有序表
private static final Object PRESENT = new Object();
public SizeBalancedTreeSet() {
this.map = new SizeBalancedTree01<>();
}
public void add(E element) {
this.map.put(element, PRESENT);
}
public int countLess(E element) {
return this.map.countLessKey(element);
}
}
public static int countRangeSum(int[] arr, int a, int b) {
if (arr == null || arr.length == 0) return 0;
int sum = 0; // 数组前缀和
int res = 0; // 结果
/*
通过改写有序表实现,有序表中每个节点加一个all属性,表示以当前节点为头节点的子树中,节点的个数,如果添加了相同的值,all也会加1
而size则表示以当前节点为头节点的子树中,不同值的节点的个数
*/
SizeBalancedTreeSet<Integer> set = new SizeBalancedTreeSet<>();
set.add(0); // 预先塞一个前缀和0
for (int i = 0; i < arr.length; i++) {
sum += arr[i];
//求sb树中小于sum - a + 1的节点个数
int count1 = set.countLess(sum - a + 1);
//求sb树中小于sum - b的节点个数
int count2 = set.countLess(sum - b);
/*
(count1 - count2)就是从0~i-1,数组累加和在[sum-b, sum-a]之间的个数
也就是以arr[i]结尾,累加和在[a, b]范围内的子数组个数
比如现在求累加和在[10, 60]范围内的子数组个数
而现在前缀和累加到100
转化为求前缀和在[40, 90]范围内的个数
在有序表中,就插小于91的个数,小于40的个数,相减,就是在[40, 90]范围内的个数
*/
res += (count1 - count2);
// 前缀和加入到集合中
set.add(sum);
}
return res;
}
}
需要改写有序表的题目二
给定一个数组arr,一个整数k表示窗口大小,窗口不断往右滑动,返回每个窗口的中位数
/**
* 给定一个数组arr,一个整数k表示窗口大小,窗口不断往右滑动,返回每个窗口的中位数
* Created by huangjunyi on 2022/9/17.
*/
public class SortedMap02 {
private static class Node implements Comparable<Node> {
private int index;
private int value;
public Node(int index, int value) {
this.index = index;
this.value = value;
}
@Override
public int compareTo(Node o) {
return this.value != o.value ? this.value - o.value : this.index - o.index;
}
}
private static class SizeBalancedTreeSet<E extends Comparable<E>> {
private SizeBalancedTree02<E, Object> map;
private static final Object PRESENT = new Object();
public E getIndex(int index) {
return this.map.getIndexKey(index);
}
public void add(E element) {
this.map.put(element, PRESENT);
}
public void remove(E element) {
this.map.remove(element);
}
public int size() {
return this.map.getSize();
}
}
public static double[] medianSlidingWindow(int[] arr, int k) {
if (arr == null || arr.length < k) return null;
// 通过改写有序表,记录窗口中结点的排序,
// 改写后的有序表,支持根据排序后的下标取值
SizeBalancedTreeSet<Node> set = new SizeBalancedTreeSet<>();
// 先把前k-1个放入窗口
for (int i = 0; i < k - 1; i++) {
set.add(new Node(i, arr[i]));
}
double[] res = new double[arr.length - k + 1];
int index = 0;
for (int i = k - 1; i < arr.length; i++) {
set.add(new Node(i, arr[i]));
/*
取出当前有序表中的排在中间的结点,该节点的值最为当前窗口的中位数,
如果是偶数个数,则取上下中位数两个节点,然后相加除2
*/
if (set.size() % 2 == 0) {
// 改写有序表后增加的方法 getIndex:根据排序后的下标取值
int v1 = set.getIndex(set.size() / 2 - 1).value;
int v2 = set.getIndex(set.size() / 2).value;
res[index++] = ((double) v1 + (double) v2) / 2;
} else {
res[index++] = set.getIndex(set.size() / 2).value;
}
set.remove(new Node(i - k + 1, arr[i - k + 1]));
}
return res;
}
}
需要改写有序表的题目三
实现一个数据结构,根据插入时序排序的数据结构(类似于ArrayList,LinkedList),支持的操作:
add(index, value) // 下标index上添加value
get(index) // 获取下标index的值
remove(index) // 删除下标index上的值
三个操作的时间复杂度都是O(logN)
还是通过改写SB树实现,但是树里面的排序不是根据key排序,而是根据插入时序排。
并且要支持插入重复值,插入的值要包装一些,以区分不同。
插入节点时,要寻找index位置在哪(往左还是往右),也是根据当前节点和左右节点的size计算得知,决定index在左边还是在右边。比如当前要在index为17位置插入一个值,当前节点size为40,左节点size为30,自然知道index为17的位置在左树上。
但是插入如果往右走时,注意index要扣掉当前节点size减去右节点size的值。
添加节点时,沿途的节点size++,所以自然时序也得到调整。
而remove的时候,沿途size–,自然时序就降下来了。
树平衡性调整,会进行平衡因子size的调整,最后是不会破坏插入时序的。
红黑树
AVL树平衡性来自左右树高差不超过1,
SB数平衡性来自叔节点size必须不少于侄节点的size,保证两棵树的节点树差不超过2被,
可见上面两种树的平衡性条件都是非常简单的。
而红黑树呢?
1、 节点不是红就是黑;
2、 头节点一定是黑;
3、 叶子节点包括空节点;
4、 叶子节点一定是黑;
5、 红节点不能相邻;
6、 每一颗子树,每一条链,黑节点数一样;
这个平衡性是怎么保证的,就不容易看出。
其实是第5、6条。因为从头节点出发,最长的链就是红黑相间,最短就是全黑,那么长度相差不超2倍。
所以平衡性也是模糊的,模糊的平衡性就是防止像AVL树那样频繁进行平衡性调整。
平衡性需要调整的情况:
插入节点有5种违规情况
删除节点有8种违规情况
一共13种违规情况,需要进行平衡性调整