Manacher算法有什么用?
Manacher算法,是一个用于快速寻找一个字符串中的最长回文子串的算法
回文就是一段文字,将它逆序之后,还是跟原来的一样,就是回文
而回文子串就是一个字符串中,连续的一段回文
比如在abc123321def中,最长回文子串就是123321
暴力解
寻找最长回文子串,暴力解:尝试每个字符往左右方向扩,直到扩不动




但是当回文是偶数长度时,这种方法是有问题的:

没有办法指到cc中间的虚轴,因此得不到最长回文子串长度为4的结果
解决办法是中间添加一个分割符,例如#:
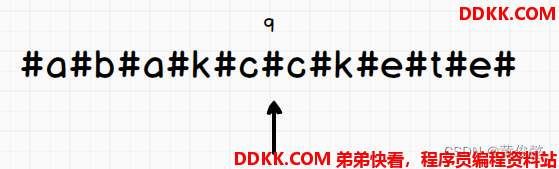
添加中间分隔符后,就可以指到代表虚轴的#字符,cc中间的#,可以扩到9长度
9/2,最是对应在原字符串中最长回文子串kcck的长度4
这种暴力方法是O(N^2)的时间复杂度
而Manacher是O(N)时间复杂度
前置概念
回文直径 回文半径
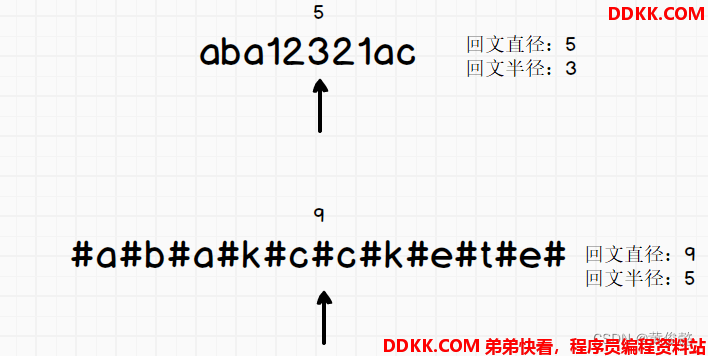
回文半径数组
记录每个字符扩展时,扩出的回文半径长度
从左往右求每个位置的回文半径,记到数组里去
最右回文边界
intR = -1
一开始最右回文半径边界在-1,因为还没开始扩

intR = 0
第一个字符,回文半径是0,所以最右回文半径到0位置

intR = 2
第二个字符,回文半径是2,所以最右回文半径到2位置

intR = 4
第三个字符,回文半径是3,所以最右回文半径到4位置

intR = 4
第4个字符,回文半径是2,没有突破右边界,所以没有更新

intR = 4
第5个字符,回文半径是0,没有突破右边界,所以没有更新

intR = 10
第6个字符,回文半径是6,更新为10
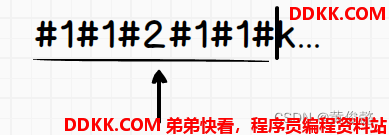
取得最右回文边界的中心点
就是取得一个最右回文边界时,是从哪个中心点开始扩的,更新最右回文半径R的时候,要同时更新最右回文边界中心点C

Manacher算法求解过程
假设遍历到i位置字符,有两种条件:
1)i没被R罩住
2)i被R罩住
如果i位置字符没有被R罩住,不优化,暴力扩
i位置字符被R罩住,则可以优化,且有三种细分情况
如果i被罩住,就存在拓扑关系:
i在C和R中间
存在C左边对称点i、

2、 1)i、扩出的区域在LR内;
很明显,这种情况i扩得的区域,肯定和i、一样,所以i不用尝试扩,取i、的值
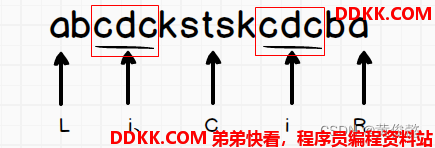
2、 2)i、扩出的区域在LR外;
这种情况下,i最多就只能扩到R停下,所以i不用尝试扩,回文半径就是i~R

2、 3)i、扩出的区域,左边界和L压线;
这种情况下,i是有一段区域不用验的,就是和i、扩出的等长的区域,但i是有可能还能继续扩的

总结:

时间复杂度:

代码
/**
* 给定一个字符串,求出它的最长回文子串,利用Manacher算法求解
*
* Manacher算法:快速生成回文半径数组
* Created by huangjunyi on 2022/9/10.
*/
public class Manacher01 {
public static int getMaxSubPalindromeString(String str) {
if (str == null || str.length() == 0) return 0;
int r = -1; // 最大回文右边界,但是这里代表的是扩失败的位置
int c = -1; // 最大回文中心点
/*
添加代表虚轴的分割符#,返回处理串
*/
char[] chars = addSeparator(str);
// 回文半径数组
int[] rArr = new int[chars.length];
// 最大回文半径
int max = Integer.MIN_VALUE;
for (int i = 0; i < chars.length; i++) {
/*
i的回文区域是否在L~R内,如果是i的回文半径取i的值
否则i的回文半径取i~R的长度
rArr[2 * c - i]取得i的回文半径
*/
rArr[i] = r > i ? Math.min(rArr[2 * c - i], r - i) : 1;
// 如果i的回文区域与L压线,则i还可以尝试扩,如果是不需要尝试扩的情况,也会马上break
while (i + rArr[i] < chars.length && i - rArr[i] > -1) {
if (chars[i + rArr[i]] == chars[i - rArr[i]]) rArr[i]++;
else break;
}
if (i + rArr[i] > r) {
r = i + rArr[i]; // 更新最大回文右边界
c = i; // 更新最大回文中心点
}
// 每一步的回文半径,和当前的max PK一下
max = Math.max(max, rArr[i]);
}
// 最大的回文半径-1,就是原串中最长回文串长度
return max - 1;
}
private static char[] addSeparator(String str) {
char[] chars = str.toCharArray();
char[] newChars = new char[str.length() * 2 + 1];
int index = 0;
for (int i = 0; i < newChars.length; i++) {
newChars[i] = (i & 1) == 0 ? '#' : chars[index++];
}
return newChars;
}
public static void main(String[] args) {
System.out.println(getMaxSubPalindromeString("abcaaaaaacbasss"));
}
}
给定一个字符串,要求往字符串的后面补字符,使其整体变成回文串
给定一个字符串,要求往字符串的后面补字符,使其整体变成回文串
返回需要补的字符串
其实就是求必须以最后一个字符结尾的回文子串是多长,然后原字符串长度减去这个回文子串的长度,剩下的就是要补充的长度,然后把剩下这部分整体逆序,就是要补充的字符串
所以需要对Manacher算法做改进,现在不是抓住最长回文子串的长度max,而是抓住最先最早把最长回文右边界R推到字符串终止位置的中心点回文半径,记为maxContainsEnd
要在尾部补充的字符串的长度记为len,len = str.length() - maxContainsEnd + 1
那么字符串开头len长度的子串,逆序了,就是要在结尾补充的部分
/**
* 给定一个字符串,要求往字符串的后面补字符,使其整体变成回文串
* 返回需要补的字符串
* Created by huangjunyi on 2022/9/10.
*/
public class Manacher02 {
public static String process(String str) {
if (str == null || str.length() == 0) return null;
// 对字符串做处理,中间添加分隔符
char[] chars = addSeparator(str);
int r = -1; // 最长回文右边界
int c = -1; // 最长回文中心点
int[] pArr = new int[chars.length]; // 回文半径数组
int maxContainsEnd = -1; // 最长回文右边界推到字符串终止位置时的回文半径
for (int i = 0; i < chars.length; i++) {
pArr[i] = r > i ? Math.max(pArr[2 * c - i], r - i) : 1;
while (i - pArr[i] > -1 && i + pArr[i] < chars.length) {
if (chars[i - pArr[i]] == chars[i + pArr[i]]) pArr[i]++;
else break;
}
if (i + pArr[i] > r) {
r = i + pArr[i];
c = i;
}
if (r == chars.length) {
// 最长回文右边界r推到字符串终止位置了,抓住此时的回文半径,记到maxContainsEnd中,然后break
maxContainsEnd = pArr[i];
break;
}
}
// 如果maxContainsEnd位-1,表示没有回文后缀,后面要补的就是整个字符串的逆序
if (maxContainsEnd == -1) {
char[] res = new char[str.length()];
int index = 0;
for (int i = str.length() - 1; i >= 0; i--) {
res[index++] = str.charAt(i);
}
return new String(res);
}
// 算出要补充的字符串的长度
int len = str.length() - maxContainsEnd + 1;
char[] res = new char[len];
int index = 0;
// 字符串开头len长度的子串,逆序了,就是要在结尾补充的部分
for (int i = len - 1; i >= 0; i--) {
res[index++] = str.charAt(i);
}
return new String(res);
}
private static char[] addSeparator(String str) {
char[] chars = str.toCharArray();
char[] newChars = new char[chars.length * 2 + 1];
int index = 0;
for (int i = 0; i < newChars.length; i++) {
newChars[i] = (i & 1) == 0 ? '#' : chars[index++];
}
return newChars;
}
public static void main(String[] args) {
System.out.println(process("rstabccba"));
System.out.println(process("rstabccbaz"));
}
}